Asumiendo \(H_0\) cierta, la variable aleatoria \(\bar{X}\) sigue una la distribución normal con media \(\mu_0\) y desviación estándar \(\frac{\sigma}{\sqrt{n}}\).

En ella definiremos las regiones de rechazo, dividiendo la significancia \(\alpha\), en dos partes iguales.

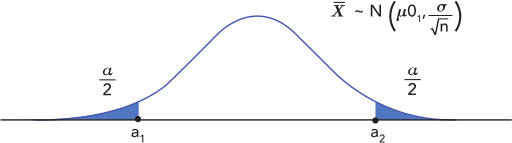
Para calcular los valores de \(a_1\) y \(a_2\) debemos partir de las probabilidades que quedan delimitadas por las respectivas regiones de rechazo.

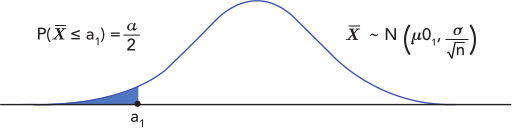
Para encontrar el valor de \(a_1\), lo primero es estandarizar.

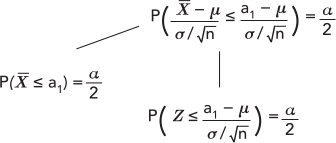
Usando una tabla de valores o un recurso, podemos encontrar el valor de \(z\) que genera una probabilidad acumulada de \(\frac{\alpha}{2} \).

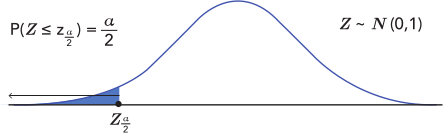
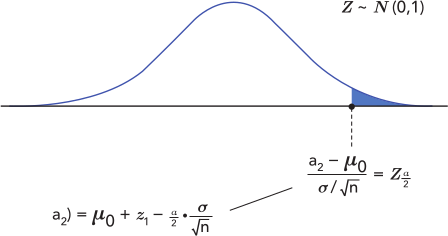
Si igualamos la fracción a \(z_{\mbox{ $\frac{\alpha}{2}$}}\) y despejamos, obtenemos el valor de \(a_1\).

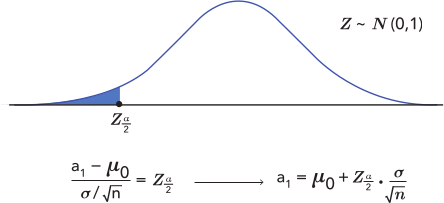
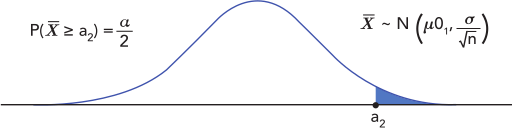
Para obtener el valor de \(a_2\) se procede de manera similar.