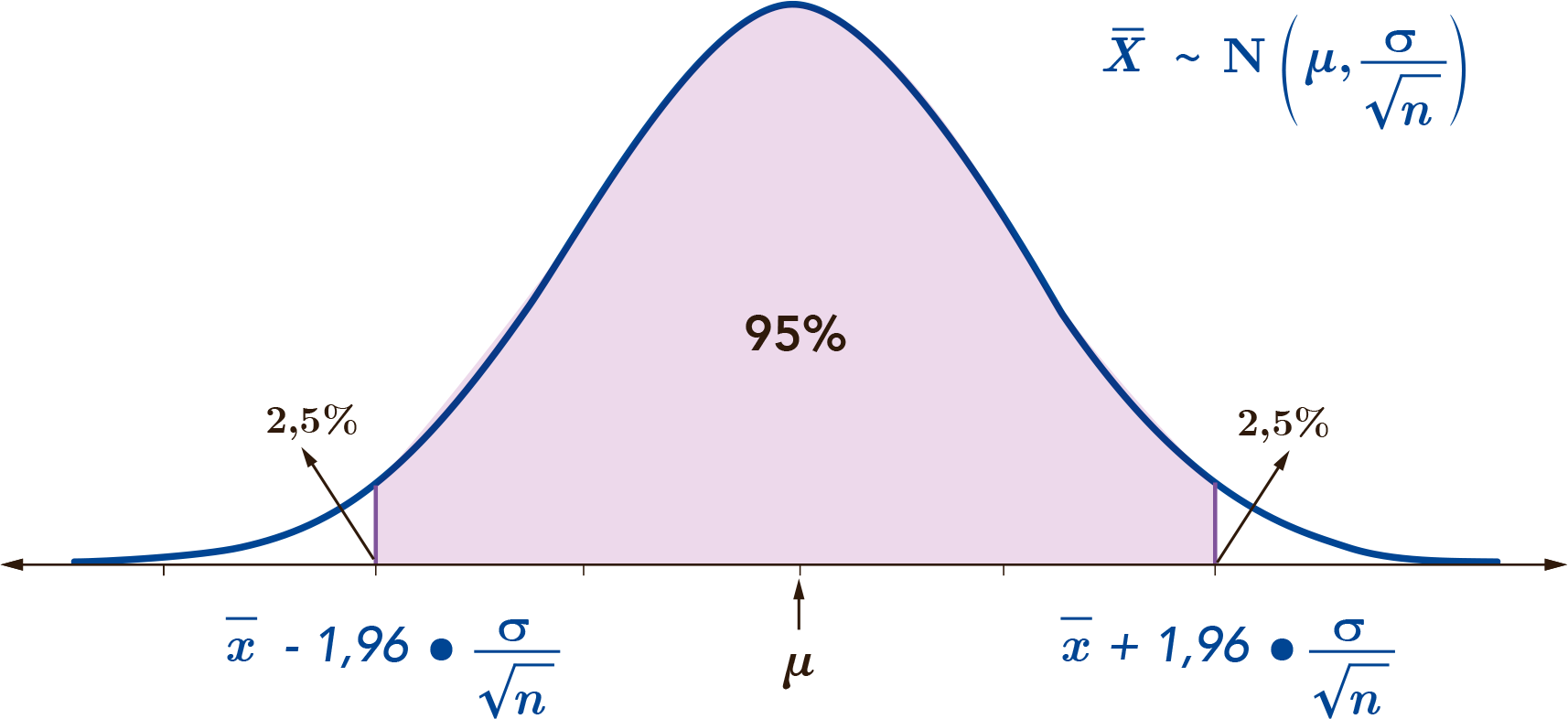
Consideremos el intervalo con un 95% de confianza para la media poblacional \(\mu\).
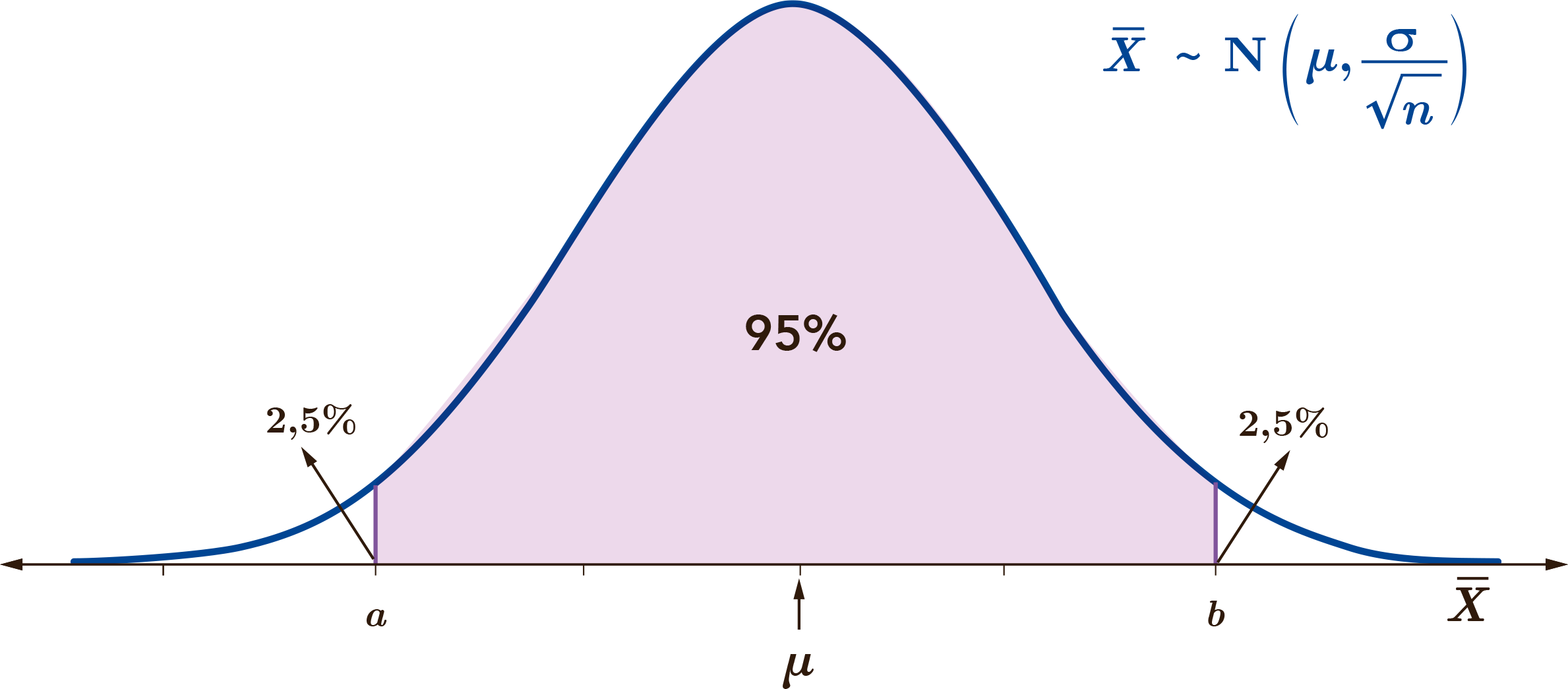
Empecemos por encontrar una expresión para el valor de \(a\). Sabemos, de acuerdo al intervalo con un 95% de confianza, que se cumple que:
\[\textrm{P}(\bar{X} \leqslant a ) = 0,\!025\]
Para conocer el valor de \(a\) que genera esta probabilidad acumulado, podemos estandarizar la variable \(\bar{X}\), expresando la probabilidad de esta forma:
\[\textrm{P} \left(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \leqslant\frac{a-\mu}{\sigma/\sqrt{n}} \right) = 0,\!025 \]
Al lado izquierdo de la desigualdad, podemos identificar la variable aleatoria estándar \(Z = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\):
\[\textrm{P} \left( Z\leqslant \frac{a-\mu}{\sigma/\sqrt{n}} \right) = 0,\!025 \]
Mediante recursos, podemos encontrar el valor \(\frac{a-\mu}{\sigma/\sqrt{n}}\) tal que genera una probabilidad acumulado de 0,025, es decir, \(z_{0,025}\), obteniendo que este valor es igual a -1,96.
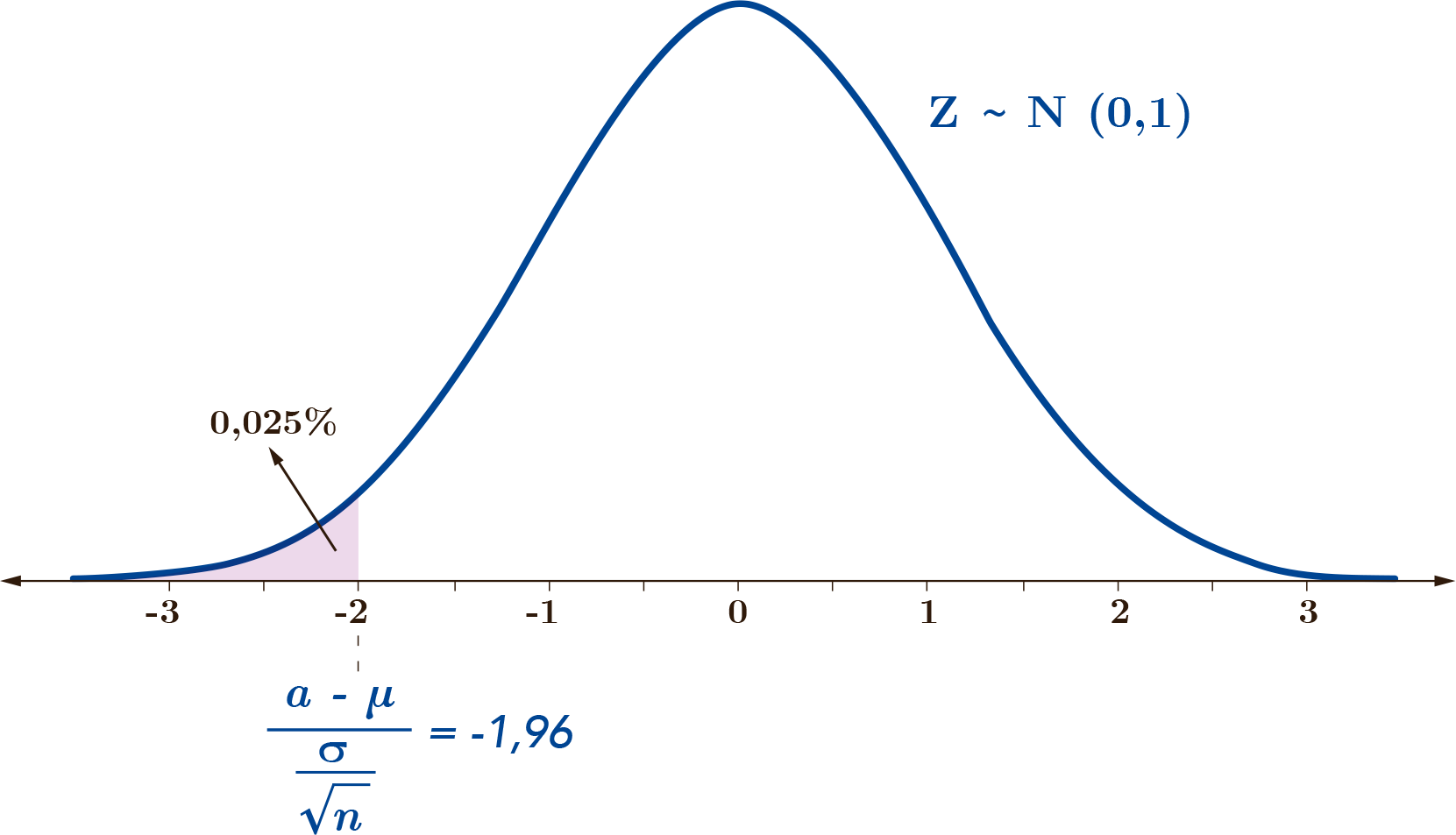
Despejando el valor de a \(a\), obtenemos:
\[a = \mu - 1,\!96 \cdot \frac {\sigma}{\sqrt{n}}\]
Realizamos el mismo procedimiento para hallar una expresión para \(b\), utilizando el hecho que la probabilidad acumulada hasta ese punto es de 0,975.
\[\textrm{P}(\bar{X} \leqslant b ) = 0,\!975\]
Luego, normalizando la variable \(\bar{X}\) como hicimos para \(a\), obtenemos el valor de \(\frac{b-\mu}{\sigma/\sqrt{n}} = 1,\!96\)
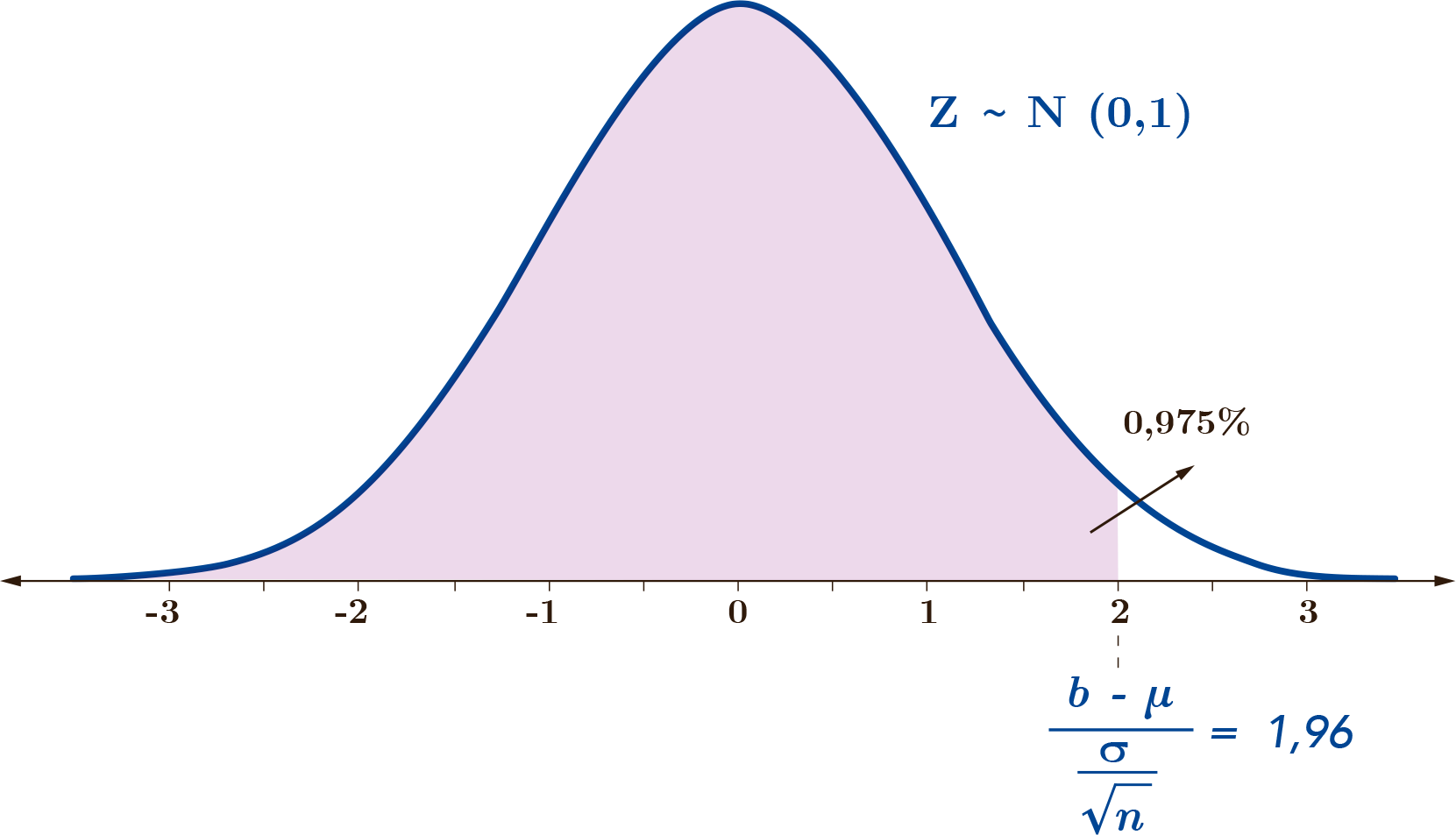
A partir de la última igualdad, podemos despejar el valor de \(b\), obteniendo que el extremo superior del intervalo:
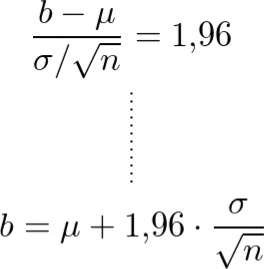
Una vez conocidas las expresiones para los valores de \(a\) y \(b\), podemos definir un intervalo con un 95% de confianza para la media muestral \(\bar{X}\):
\[\mu - 1,\!96 \cdot \frac {\sigma}{\sqrt{n}} \leqslant \bar{X} \leqslant \mu + 1,\!96 \cdot \frac {\sigma}{\sqrt{n}}\]
Reordenando los términos de la expresión, obtenemos finalmente un intervalo de 95% de confianza para la media poblacional \(\mu\):
\[\bar{X} - 1,\!96 \cdot \frac {\sigma}{\sqrt{n}} \leqslant \mu \leqslant \bar{X} + 1,\!96 \cdot \frac {\sigma}{\sqrt{n}}\]
Si extraemos de esta población una muestra de tamaño \(n\), cuyo promedio muestral es \(\bar{x}\), el intervalo se ve de la siguiente manera: