Consideremos el experimento aleatorio de lanzar \(n =3\) dados y contar el número de 4 obtenidos. En este experimento, decimos que se hacen 3 “intentos”.
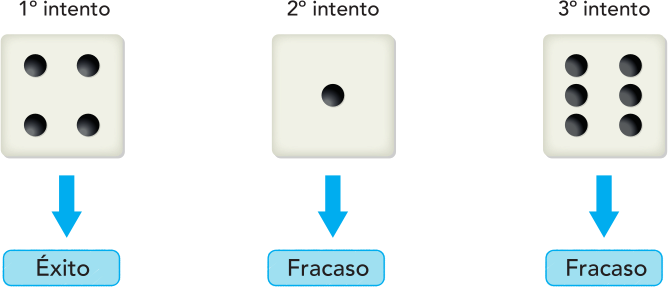
En cada intento se puede obtener un 4 (éxito), con probabilidad \(p = \frac{1}{6}\), u otro número (fracaso), con probabilidad \(1 - p = \frac{5}{6}\).
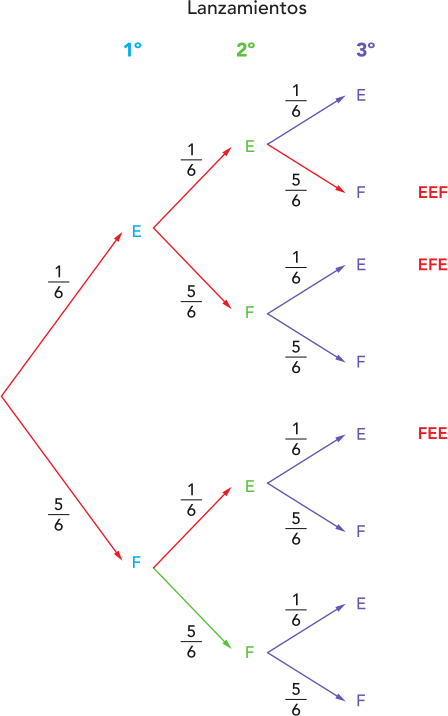
Así, por ejemplo, la probabilidad de obtener dos 4 (2 éxitos) al hacer 3 intentos es:
\[\textrm{P}(\textrm{Obtener 2 cuatros al lanzar 3 dados}) = {3 \choose 2} \cdot \left(\frac{1}{6}\right)^2 \cdot \left(\frac{5}{6}\right)^1\]
Las \({3 \choose 2} = 3\) combinaciones en las que se obtiene exactamente dos 4 se pueden visualizar en el diagrama de árbol:
Experimentos como el anterior, donde uno está interesado en observar un número particular de “éxitos” en un número definido de “intentos'', se conocen cómo experimentos binomiales.
Si definimos la variable aleatoria \(X\) cómo “el número de éxitos obtenidos en \(n\) intentos” y la probabilidad de obtener un éxito es \(p\) en cada intento, entonces decimos que \(X\) se distribuye cómo una binomial con parámetros \(n\) y \(p\), lo que denotamos así:
\[X \sim \textrm{Binomial} (n, p)\]
En un experimento Binomial, la probabilidad de obtener exactamente \(k\) éxitos en los \(n\) intentos (es decir, la probabilidad de que \(X = k\)), puede calcularse por medio de la siguiente fórmula:

En esta fórmula, el factor \(p^k\) corresponde a la ocurrencia de \(k\) éxitos y el factor \((1-p)^{n-k}\) corresponde a los fracasos, que ocurren \(n-k\) veces. El número combinatorio corresponde a que la ocurrencia de \(k\) éxitos y \(n-k\) fracasos se puede dar exactamente de \({n \choose k}\) maneras.