Nicolás quiere contestar cada una de las 10 preguntas de una prueba al azar. Considera la variable aleatoria \(W_i\) definida cómo “Nicolás contesta la pregunta \(i\) correctamente”. Supón que Nicolás contesta la prueba de la siguiente forma:

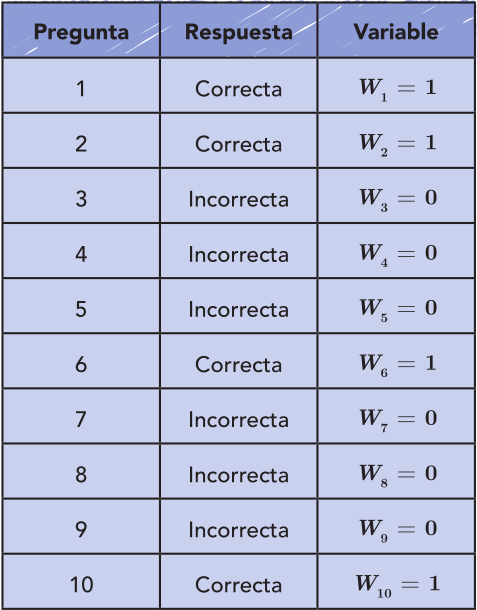
Fíjate como la suma de todas las variables \(W_i\) te da el número de preguntas que Nicolás contestó correctamente.

Resumamos algunas de las ideas más relevantes sobre las variables \(N\) y \(W_i\):

• Cada vez que Nicolás contesta una pregunta al azar tenemos un experimento Bernoulli con probabilidad de éxito \(p=\frac{1}{4}\). Por lo tanto,

  \[W_i \sim \textrm{Bernoulli} \left(p = \frac{1}{4}\right)\]

• Estos experimentos Bernoulli son independientes, ya que estamos suponiendo que lo que Nicolás contesta en una pregunta no afecta a cómo contestará las demás preguntas.
• Contestar la prueba completa al azar representa la repetición de un experimento Bernoulli 10 veces (la prueba tiene 10 preguntas).
• La variable \(N\) definida cómo “el número de preguntas que Nicolás contestó correctamente” corresponde a:

  \[N = W_1 + W_2 + W_3 + \cdots + W_{10}\]

Notemos que en el caso de la tabla anterior, se tiene que \(N = 4\) ya que:

\(N = 1+1+0+0+0+1+0+0+0+1 = 4\)

Contar el número de preguntas que Nicolás contestó correctamente entre las 10 preguntas que tenía la prueba es un experimento binomial, pues corresponde a observar el número de éxitos (preguntas correctas) de un total de 10 intentos (preguntas en la prueba). Como la probabilidad de éxito (pregunta es correcta) es \(\frac{1}{4}\), entonces tenemos que:

\[N \sim \textrm{Binomial} \left(n = 10, p = \frac{1}{4}\right)\]

Si tenemos \(n\) variables aleatorias Bernoulli, \(W_1, W_2, \dots, W_{n}\), donde cada una de ellas tiene probabilidad de éxito \(p\) y es independiente de las otras variables, y definimos \(X\) como la suma de estas \(n\) variables de Bernoulli, entonces:

\[X =W_1 + W_2 + \cdots + W_n \sim \textrm{Binomial } (n, p)\]