El valor esperado de una variable aleatoria $Y$ corresponde al valor promedio teórico de la variable y se denota por $\textrm{E}(Y)$, para diferenciarlo de la media o promedio muestral que usualmente se denota por $\bar{Y}$.

Como ejemplo, para el “Juego de los dados” definimos la variable aleatoria discreta $Y$: “monto obtenido al lanzar una vez los dados”. Supón que repetimos este experimento 50 veces (muestra), obteniendo los siguientes resultados:

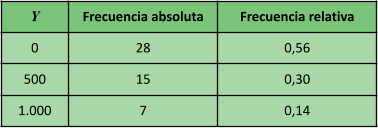
Calculemos el promedio muestral utilizando las frecuencias absolutas:

$\begin{align*} \bar{Y} &= \frac{0 \cdot 28 + 500 \cdot 15 + 1.000 \cdot 7}{50} \\ &= 0 \cdot \frac{28}{50} + 500 \cdot \frac{15}{50} + 1.000 \cdot \frac{7}{50} \\ &= 0 \cdot 0,\!56 + 500 \cdot 0,\!30 + 1.000 \cdot 0,\!14 \\ &= 290 \end{align*}$

Observa que en el cálculo aparecieron las frecuencias relativas. El valor que obtuvimos nos indica que, luego de jugar 50 partidas, el jugador ganó un promedio de $290.

Para determinar el valor esperado $\textrm{E}(Y)$ seguimos la misma idea, solo que en lugar de utilizar frecuencias relativas de una muestra, utilizaremos las probabilidades teóricas $\textrm{P}(Y = k)$ de cada valor $k$ que puede tomar $Y$.

Estas se calculan a partir de los casos favorables de cada evento “$Y = k$” como muestra el diagrama.

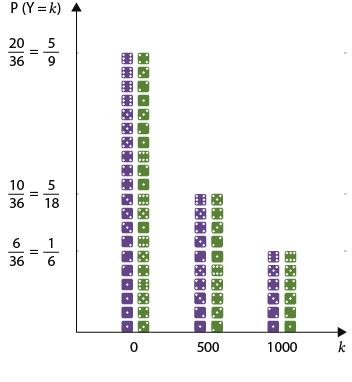
Ahora calculamos $\textrm{E}(Y)$ usando la probabilidad de cada valor de $Y$:

$ \begin{align*} \textrm{E}(Y) &= 0 \cdot \textrm{P}(Y = 0) + 500 \cdot \textrm{P}(Y = 500) + 1.000 \cdot \textrm{P}(Y = 1.000) \\ &= 0 \cdot \frac{5}{9} + 500 \cdot \frac{5}{18} + 1.000 \cdot \frac{1}{6} \\ &\approx 306 \end{align*} $

Este valor nos indica que si este juego se repite un número muy grande de veces, un jugador espera ganar aproximadamente $306 en promedio por partida (de ahí el nombre “valor esperado”).

Entonces, si la variable aleatoria discreta $Y$ puede tomar los valores $k_1, k_2, \ldots, k_n$, cada uno con probabilidades $\textrm{P}(Y = k_1), \textrm{P}(Y = k_2), \ldots, \textrm{P}(Y = k_n)$, el valor esperado $\textrm{E}(Y)$ se calcula de la siguiente forma:

\[ \textrm{E}(Y) = k_1 \cdot \textrm{P}(Y = k_1) +k_2 \cdot \textrm{P}(Y = k_2) + \cdots + k_n \cdot \textrm{P}(Y = k_n) \]

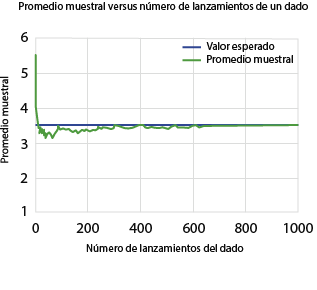
Entonces, $\bar{Y}$ es el promedio muestral y $\textrm{E}(Y)$ es el promedio teórico del experimento aleatorio. Sus valores no siempre coinciden, pero el valor de $\bar{Y}$ se aproxima al valor de $\textrm{E}(Y)$ a medida que el experimento se repite más veces.

El siguiente gráfico muestra cómo $\bar{Y}$ se aproxima al valor de $\textrm{E}(Y)$ (línea horizontal) a medida que crece el número de lanzamientos.