El valor esperado tiene importantes propiedades, las cuales vamos a discutir aquí. Para eso, vamos a retomar la situación de la PYME que vendía accesorios para teléfonos inteligentes. La variable aleatoria \(N\) representa “el número de pedidos online que recibe esta PYME en un día” y tiene la siguiente función de probabilidad:
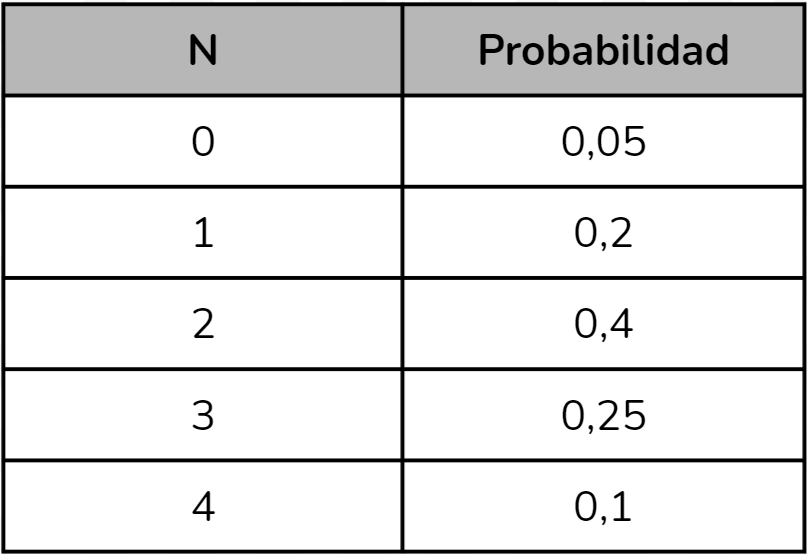
El valor esperado de pedidos online en un día cualquiera puede determinarse con el siguiente cálculo:
\(\begin{align*} \textrm{E}(N) &= 0 \cdot 0,\!05 + 1 \cdot 0,\!2 + 2 \cdot 0,\!4 + 3 \cdot 0,\!25 + 4 \cdot 0,\!1 \\ &= 0 + 0,\!2 + 0,\!2 + 0,\!8 + 0,\!75 + 0,\!4 \\ &= 2,\!15 \end{align*}\)
Este valor indica que, en un día cualquiera, la empresa espera recibir aproximadamente 2 pedidos online.
La empresa debe estimar el costo por delivery para entregar los productos pedidos. El servicio que ellos prefieren les cobra una tarifa fija de \($2\,000\) y una tarifa variable de \($850\) por cada artículo a ser despachado.
Definamos la variable aleatoria \(C = 2\,000 + 850 \cdot X\) como “el costo por el servicio de delivery para los pedidos online de un día”, y calculemos sus valores:
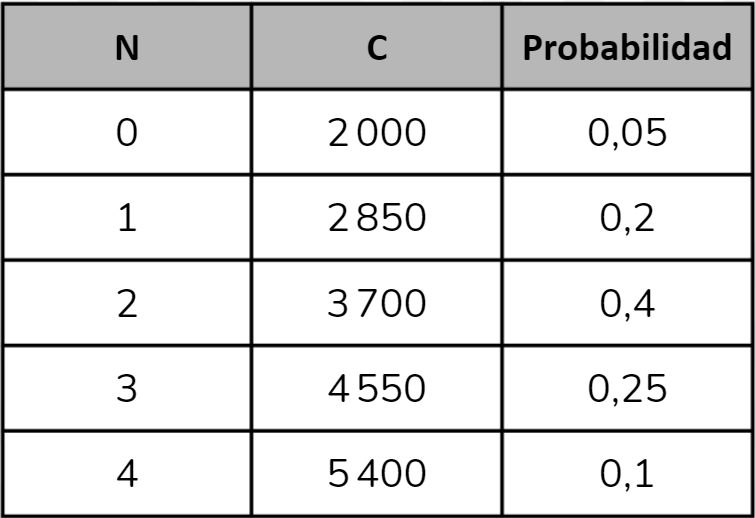
Para calcular el costo que la empresa espera pagar por servicio de delivery en un día cualquiera \(\textrm{E}(C)\). Primero, vamos a calcular \(\textrm{E}(C)\) en la forma que ya conoces:
\(\begin{align*} \textrm{E}(C) &= 2\,000 \cdot 0,\!05 + 2\,850 \cdot 0,\!2 + 3\,700 \cdot 0,\!4 + 4\,550 \cdot 0,\!25 + 5\,400 \cdot 0,\!1 \\ &= 100 + 570 + 1\,480 + 1\,137,\!5 + 540 \\ &= 3\,827,\!5 \end{align*}\)
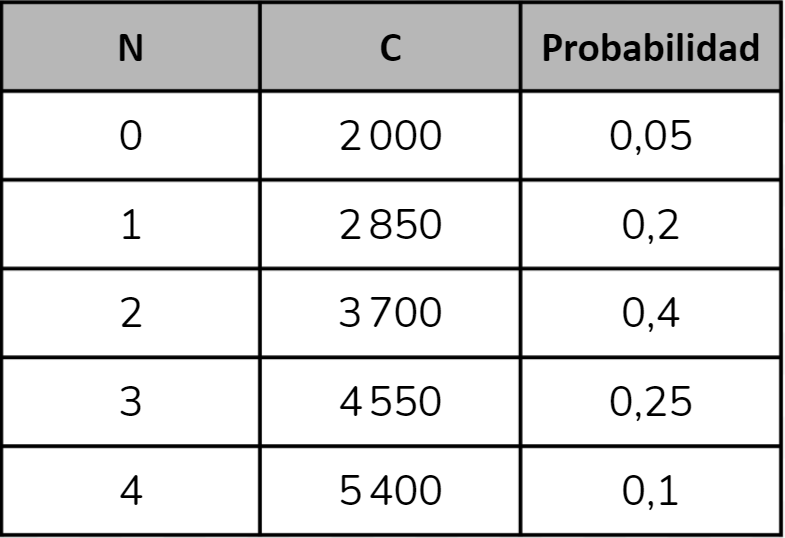
Otra forma de calcular el costo esperado \(\textrm{E}(C)\) es la siguiente. Sabemos que la empresa espera recibir \(\textrm{E}(X) = 2,\!15\) pedidos online en un día. Por lo tanto, el costo esperado por delivery en un día cualquiera sería el siguiente:
\(\begin{align*} \textrm{E}(C) &= 2\,000 + 850 \cdot \textrm{E}(X) \\ &= 2\,000 + 850 \cdot 2,\!15 \\ &= 3\,827,\!5 \end{align*}\)
Esta es una propiedad importante del valor esperado: Si tenemos una variable aleatoria \(X\) y tenemos otra variable aleatoria \(Y = a \cdot X + b\) (es decir, \(Y\) es una función lineal de \(X\)). Entonces:
\(\textrm{E}(Y) = E (a \cdot X + b ) = a \cdot \textrm{E}(X) + b\)
Este resultado se puede generalizar de la siguiente forma. Si la variable aleatoria \(X\) toma los valores \(k_1, k_2, \ldots, k_n\), cada uno con probabilidad \(\textrm{P}(X = k_1), \textrm{P}(X = k_2), \ldots, \textrm{P}(X = k_n)\), respectivamente, y tenemos la variable aleatoria \(Y = g(X)\). Entonces:
\[\textrm{E}(Y) = E (g(X)) = g(k_1) \cdot \textrm{P}(X = k_1) + g(k_2) \cdot \textrm{P}(X = k_2) + \cdots + g(k_n) \cdot \textrm{P}(X = k_n) \]
El valor esperado de una variable aleatoria también tiene estas otras propiedades importantes, tales como:
- Valor esperado de una constante \(c\):
\(\textrm{E}(c) = c\) - Valor esperado de la suma de variables aleatorias \(X_1, X_2, \ldots, X_n\):
\(\textrm{E}(X_1 + X_2 + \ldots + X_n) = \textrm{E}(X_1) + \textrm{E}(X_2) + \ldots + \textrm{E}(X_n)\) - Valor esperado de combinaciones lineales de dos variables aleatorias \(X\) y \(Y\):
\(\textrm{E}(a \cdot X + b \cdot Y) = a \cdot \textrm{E}(X) + b \cdot \textrm{E}(Y)\)