La idea fundamental detrás de la regresión lineal es cómo encontrar la recta que describa de mejor forma la relación entre dos variables \(x\) e \(y\) cuando se cree que esta puede ser lineal.
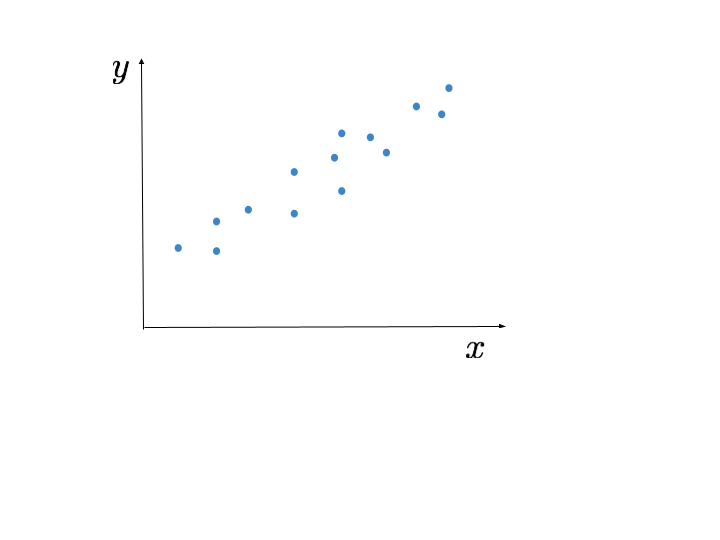
La relación entre estas variables la podemos describir por la ecuación \(y = \beta_1 \cdot x + \beta_0\).
Los coeficientes \(\beta_1\) y \(\beta_0\) se conocen como parámetros del modelo y en general son desconocidos.

Sin embargo, estos parámetros se pueden estimar a partir de datos empíricos.
Para ello, se toman datos y, utilizando el método de los mínimos cuadrados, se encuentra la recta que se ajuste mejor a los datos, es decir, la que pase “más cerca” de todos los puntos.
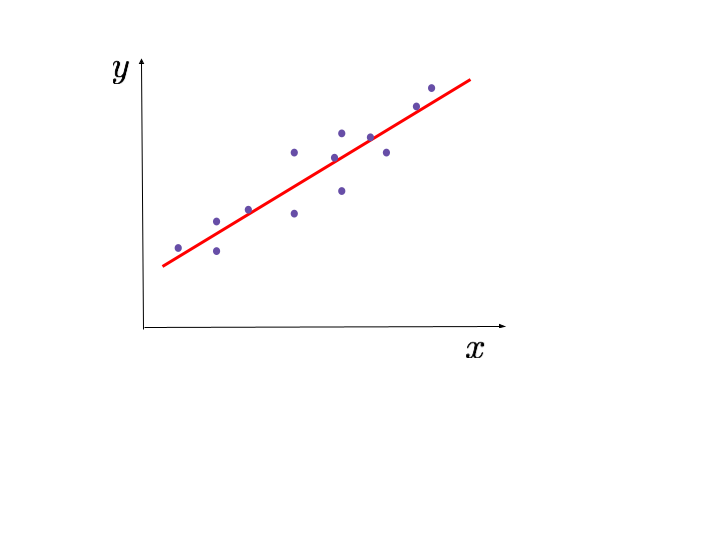
La recta que encontramos al aplicar este método la denotamos como: \(\hat{y} = \hat{\beta}_1 \cdot x + \hat{\beta}_0\).
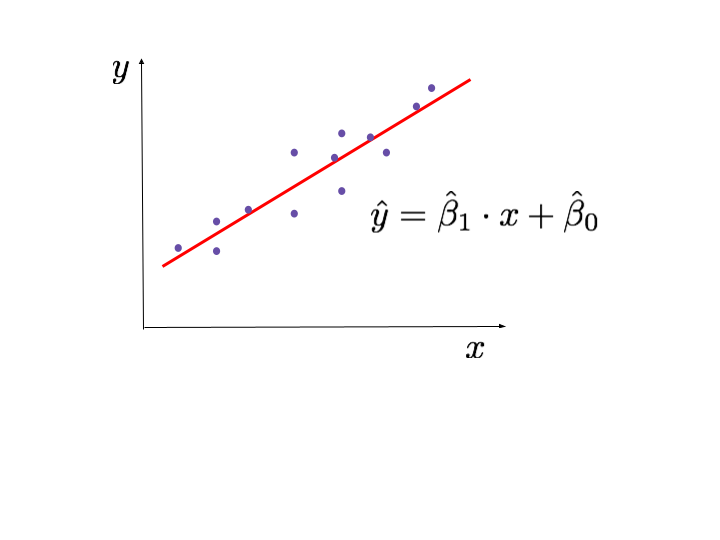
Como esta recta constituye un modelo que estima la relación entre las variables a partir de un conjunto de datos, decimos que los coeficientes \(\hat{\beta}_1\) y \(\hat{\beta}_0\) son estimadores de los parámetros del modelo.
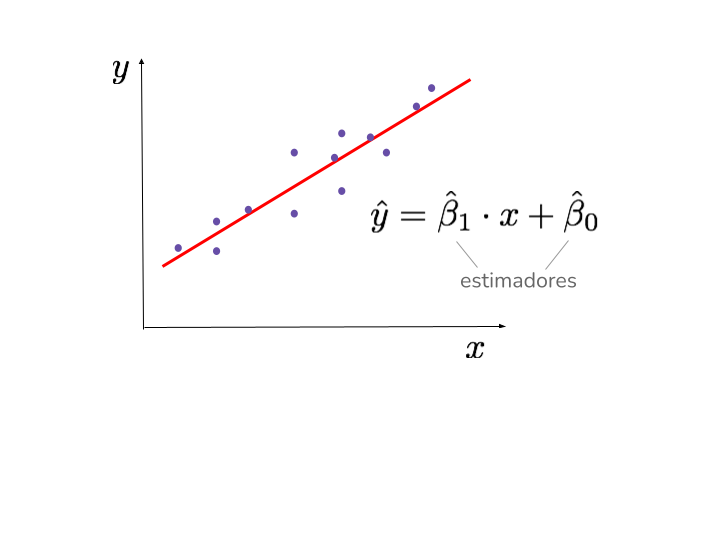
Es importante tener en cuenta que si aplicamos el método de mínimos cuadrados a otra muestra, los estimadores que se obtienen pueden ser distintos.

Debido a la variabilidad y los errores propios de un fenómeno aleatorio, no es posible encontrar los “verdaderos” valores de los parámetros \(\beta_1\) y \(\beta_0\) del modelo de regresión.
Sin embargo, si se cuenta con un conjunto de datos que cumple ciertas condiciones, el método de mínimos cuadrados entrega una muy buena estimación de estos parámetros.
