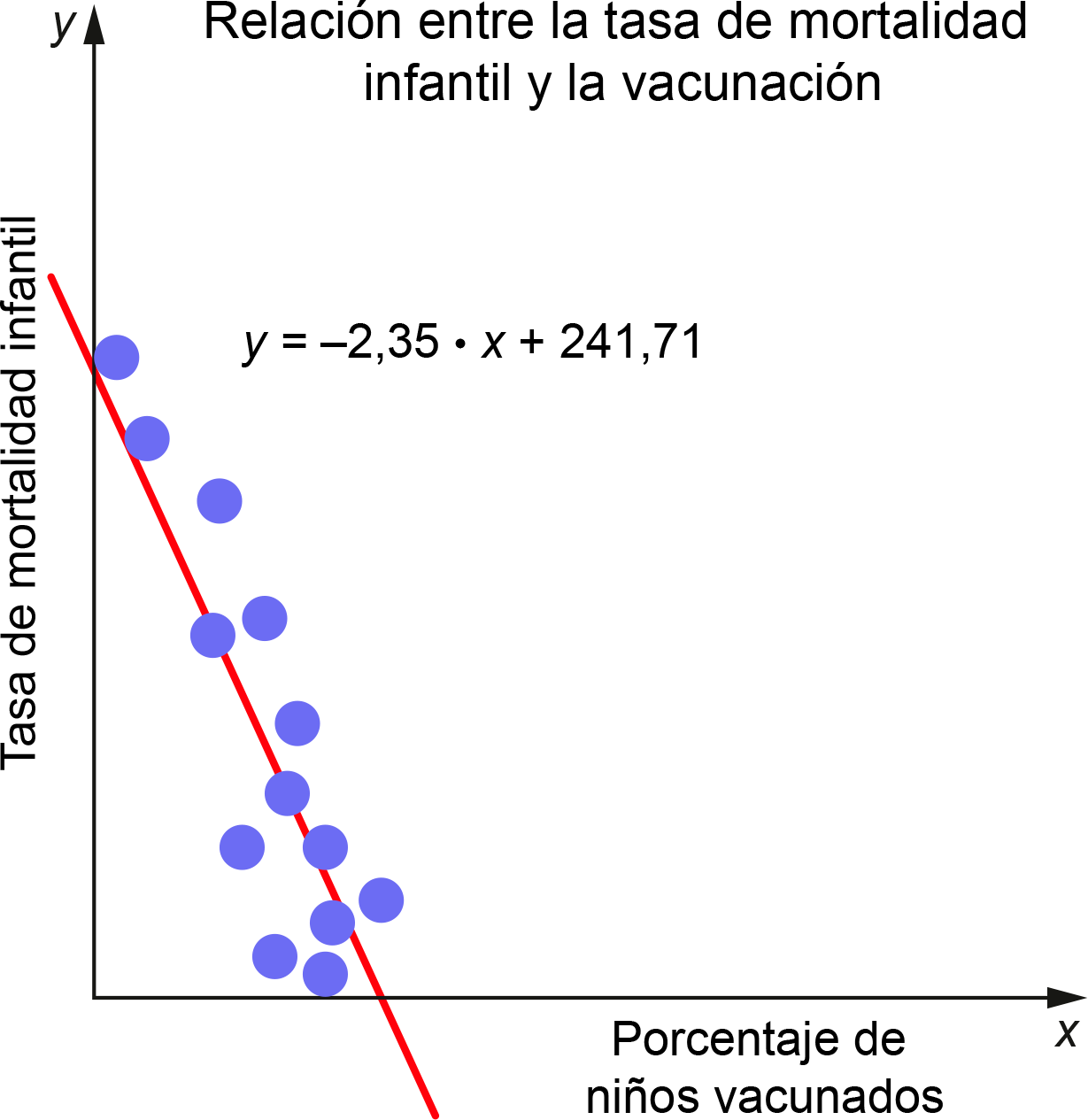
Si en un gráfico de dispersión los puntos siguen una tendencia lineal, podemos representar el patrón mediante una recta que está cerca de los puntos.

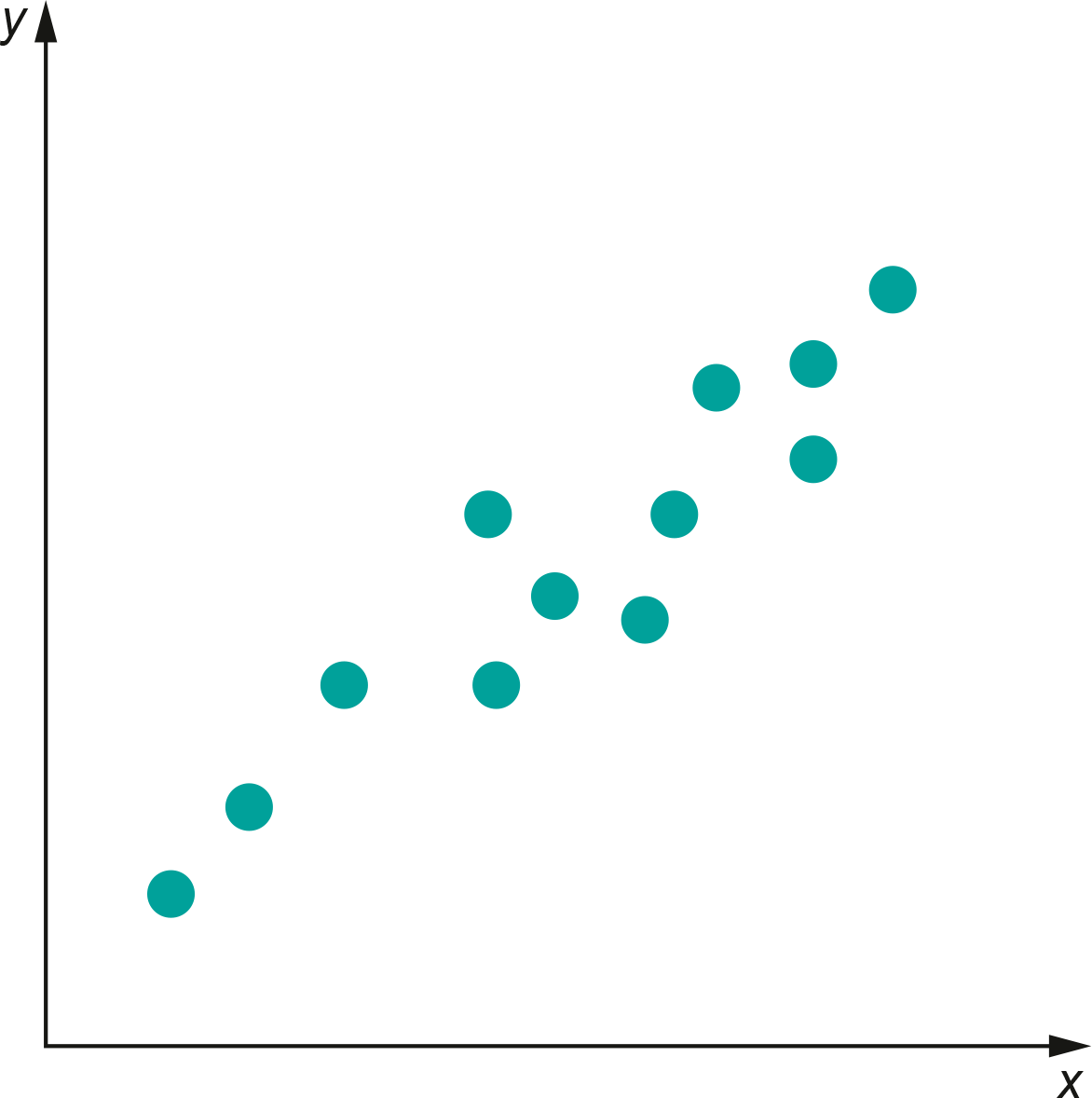
Esta recta modela la relación entre las variables \(x\) e \(y\) para los datos y puede resultar útil para estimar el valor de una a partir de la otra.

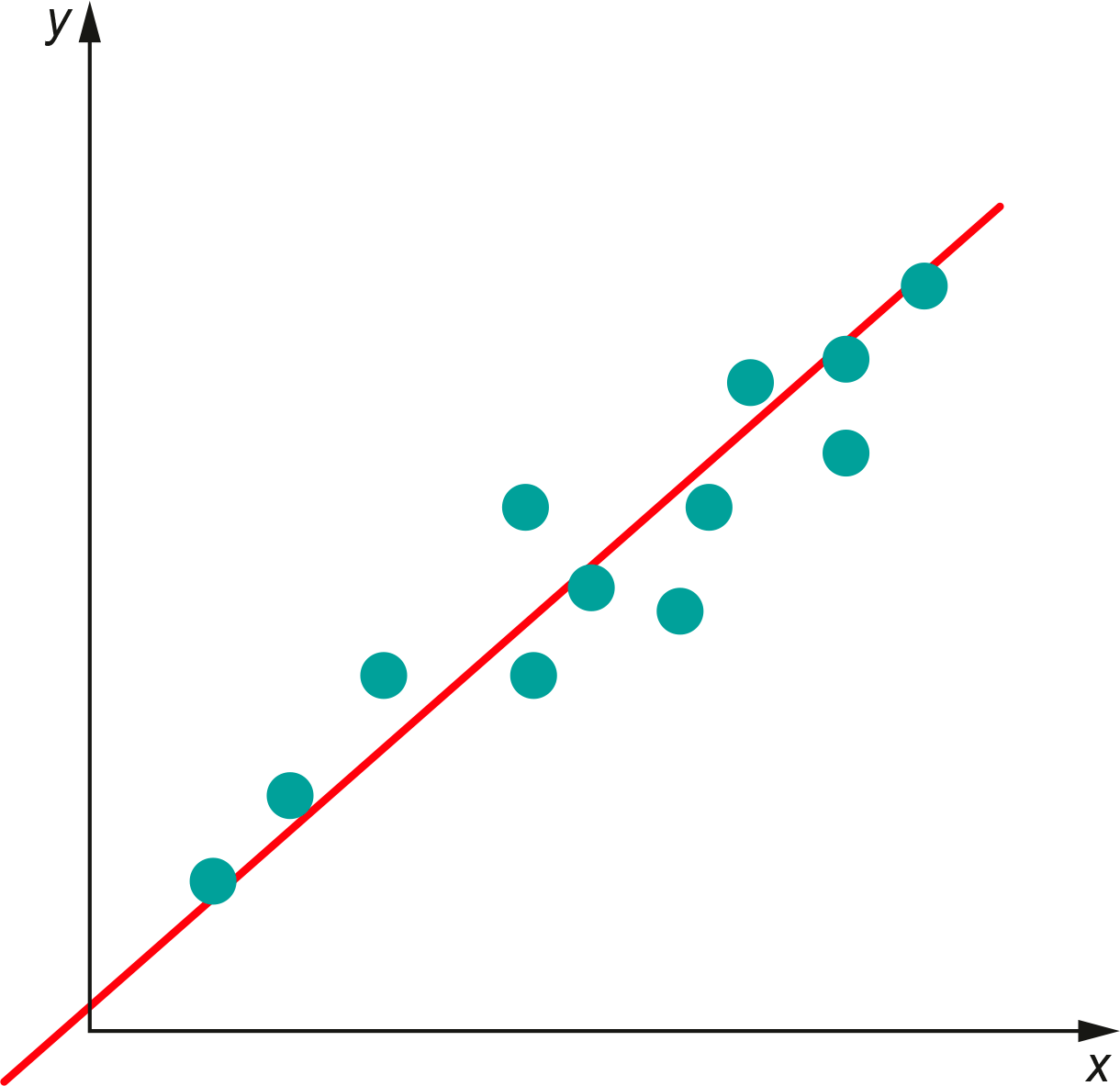
La recta que modela los datos podemos describirla mediante la ecuación:

\(y = m\cdot x + n\)

Donde \(m\) es la pendiente y \(n\) es el coeficiente de posición de la recta.

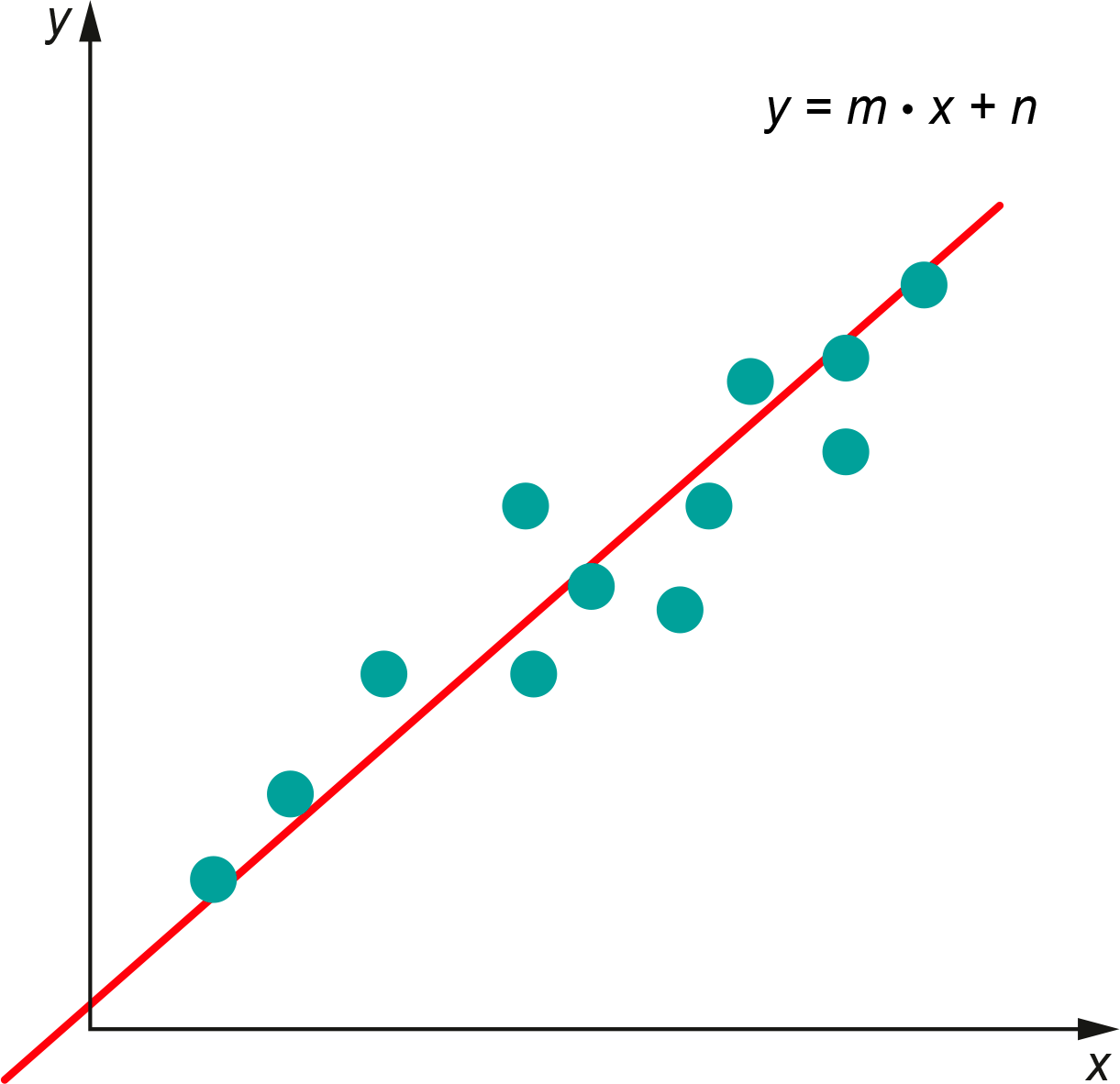
Si al aumentar la variable \(x\)  la variable \(y\) también aumenta, la pendiente de la recta es positiva y por tanto decimos que la relación entre las variables sigue una tendencia lineal positiva.

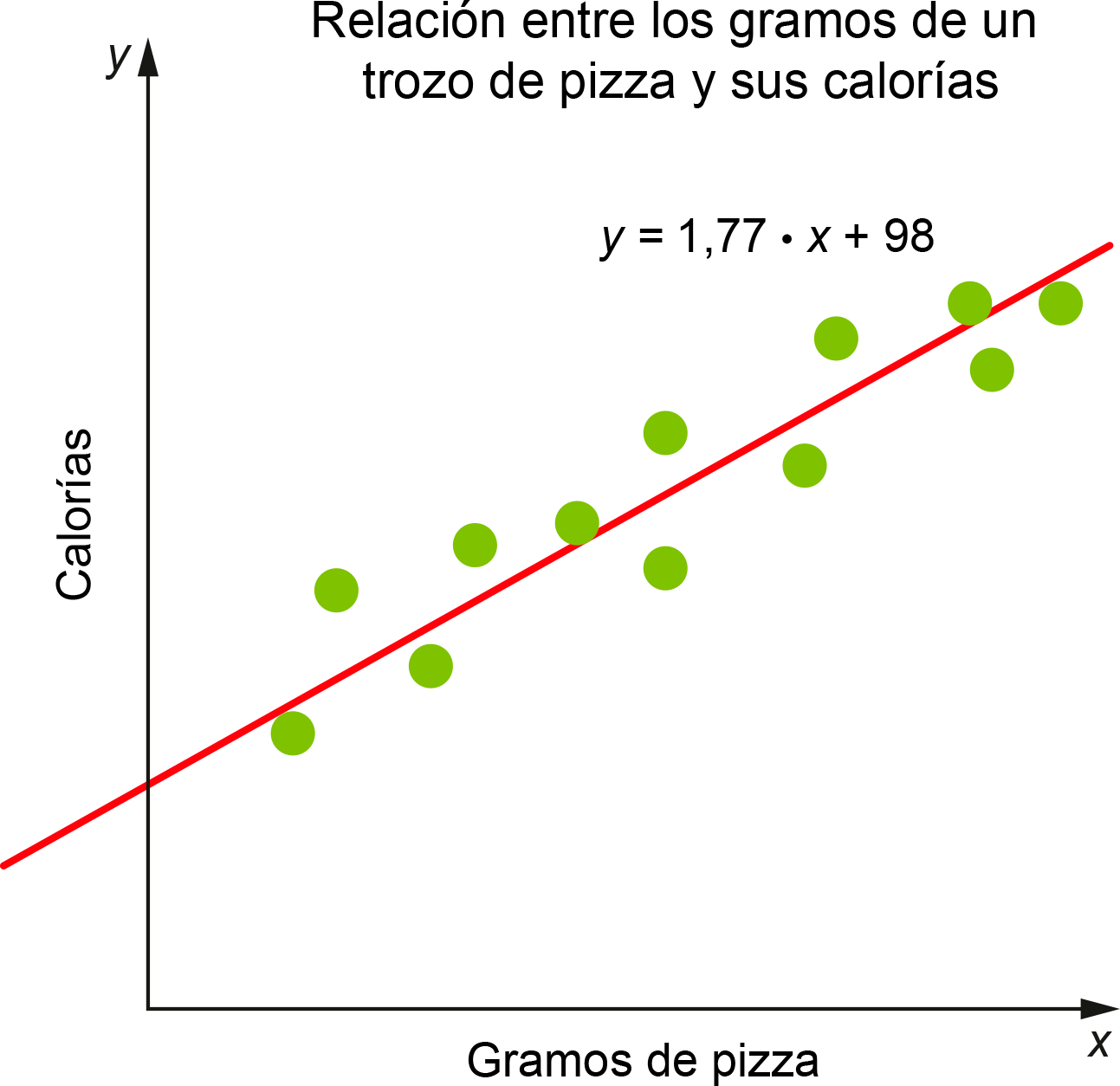
Por otro lado, si al aumentar la variable \(x\), la variable \(y\) disminuye, la pendiente de la recta es negativa.  En tal caso decimos que la relación entre las variables sigue una tendencia lineal negativa.