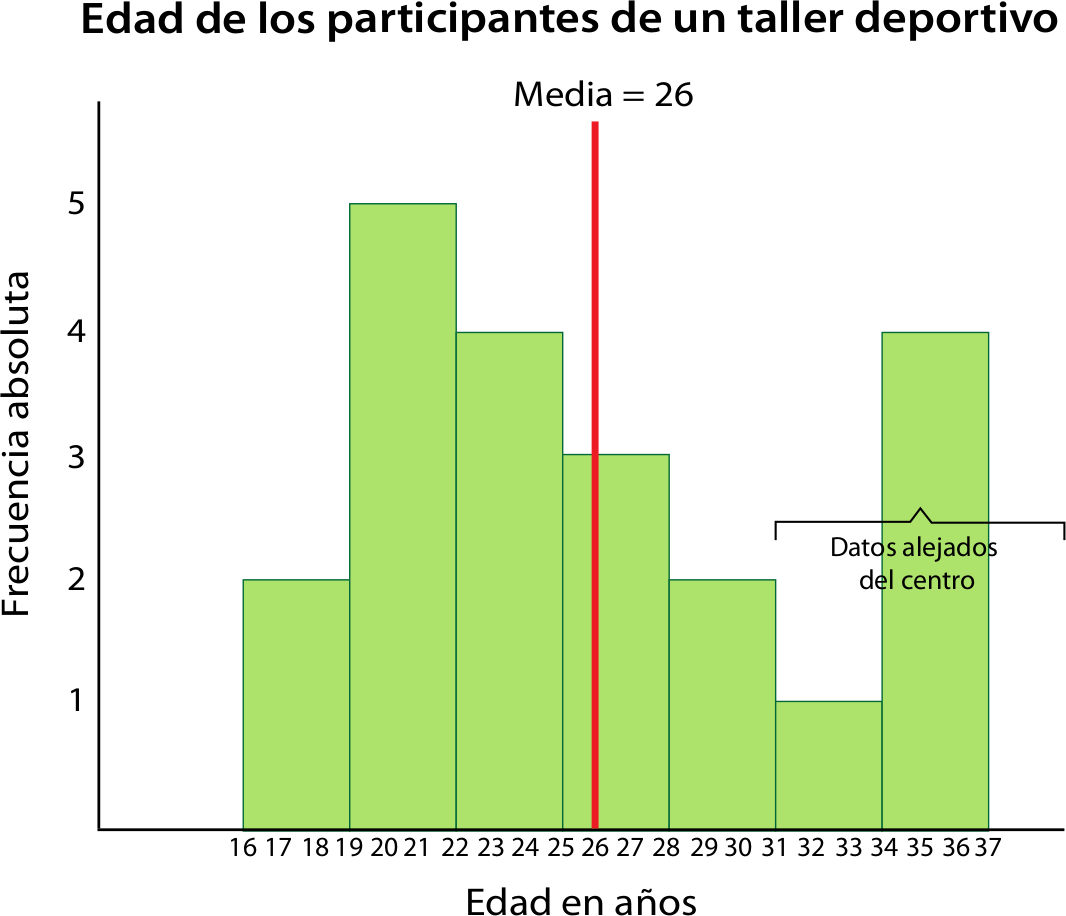
La media o promedio de un conjunto de datos se obtiene al sumarlos todos y luego dividir lo obtenido por el número de datos. Una manera de interpretar la media es considerarla como el punto de equilibrio de todos los datos. En el ejemplo, la media de las edades de los participantes del taller es 26, que es la edad donde se equilibran los datos, como se observa en el diagrama de puntos.
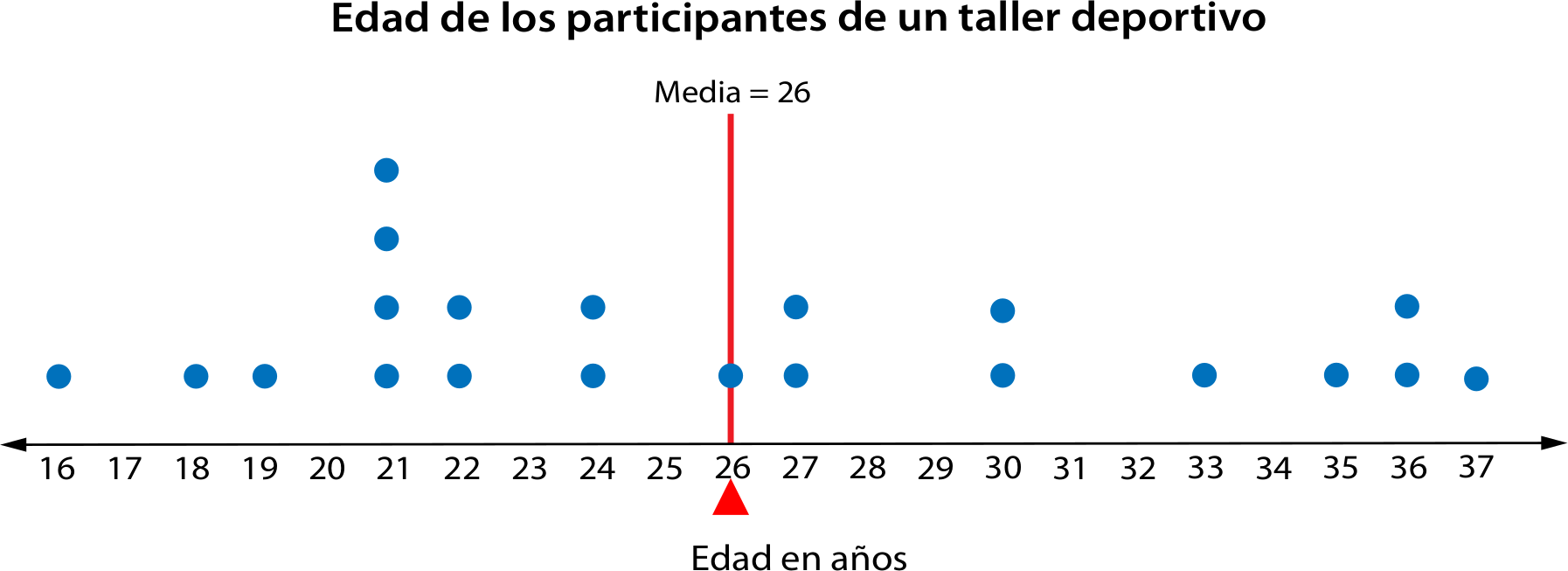
La media se puede considerar como un punto de equilibrio, es decir, como el número tal que la suma de las distancias desde este a los datos menores que él es igual a la suma de las distancias desde este a los datos que son mayores. En el ejemplo vemos que la distancia desde el 21 a la media es de cinco unidades y la distancia desde el 27 a la media es una unidad.
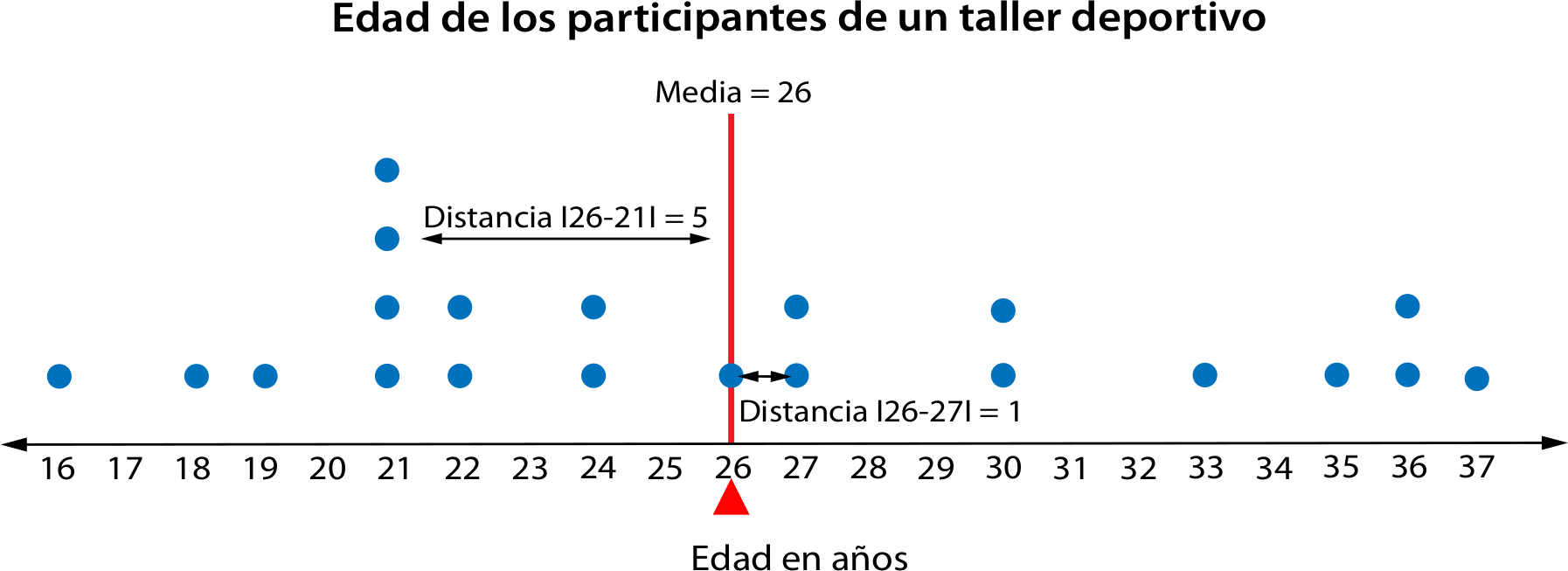
La siguiente tabla muestra que se cumple que la suma de las distancias entre la media y los datos que son menores que ella es igual a la suma de las distancias entre la media y los datos que son mayores a ella.
\(1\times|26-16|=10\)
\(2\times|26-27|=2\)
\(1\times|26-18|=8\)
\(4\times|26-30|=8\)
\(1\times|26-19|=7\)
\(1\times|26-33|=7\)
\(4\times|26-21|=20\)
\(1\times|26-35|=9\)
\(2\times|26-22|=8\)
\(2\times|26 - 36|=20\)
\(2\times|26-24|=4\)
\(1\times|26-37|=11\)
Suma = \(57\)
Suma = \(57\)
De la misma forma, cuando los datos están representados en un histograma, la media podemos pensarla como el punto de equilibrio de los datos, en este caso representados por las barras del histograma.
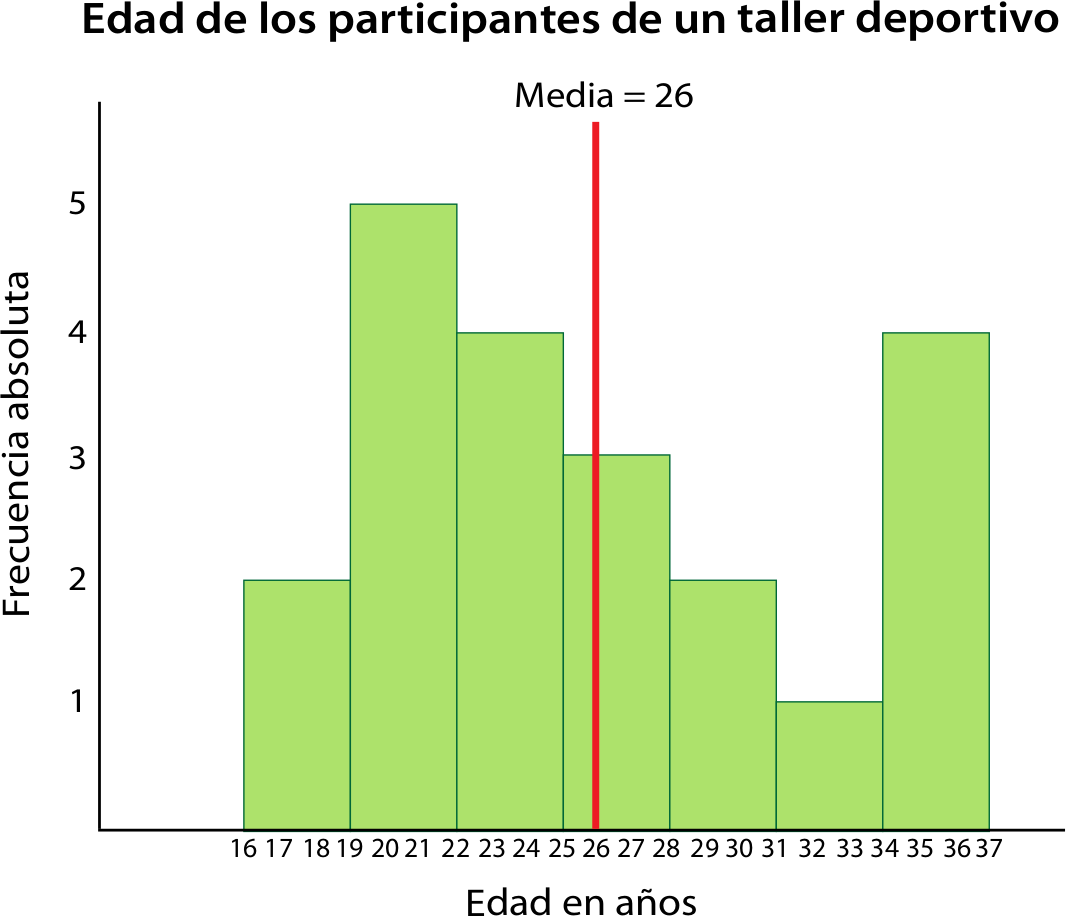
Una característica de la media como medida de tendencia central es que es más sensible a datos que están alejados del centro de la distribución.